College Algebra Textbook, Test Bank

College Algebra TextBook by OpenStax plus MCQ, Essay Questions & Key Terms

College Algebra provides a comprehensive exploration of algebraic principles and meets scope and sequence requirements for a typical introductory algebra course. The modular approach and richness of content ensure that the book meets the needs of a variety of courses. College Algebra offers a wealth of examples with detailed, conceptual explanations, building a strong foundation in the material before asking students to apply what they’ve learned.

* Complete Textbook by OpenStax

* Multiple Choices Questions (MCQ)

* Essay Questions Flash Cards

* Key-Terms Flash Cards

Powered by QuizOver.com the leading online quiz creator

https://www.quizover.com

1. Prerequisites

Introduction to Prerequisites

1.1. Real Numbers: Algebra Essentials

1.2. Exponents and Scientific Notation

1.3. Radicals and Rational Exponents

1.4. Polynomials

1.5. Factoring Polynomials

1.6. Rational Expressions

2. Equations and Inequalities

Introduction to Equations and Inequalities

2.1. The Rectangular Coordinate Systems and Graphs

2.2. Linear Equations in One Variable

2.3. Models and Applications

2.4. Complex Numbers

2.5. Quadratic Equations

2.6. Other Types of Equations

2.7. Linear Inequalities and Absolute Value Inequalities

3. Functions

Introduction to Functions

3.1. Functions and Function Notation

3.2. Domain and Range

3.3. Rates of Change and Behavior of Graphs

3.4. Composition of Functions

3.5. Transformation of Functions

3.6. Absolute Value Functions

3.7. Inverse Functions

4. Linear Functions

Introduction to Linear Functions

4.1. Linear Functions

4.2. Modeling with Linear Functions

4.3. Fitting Linear Models to Data

5. Polynomial and Rational Functions

Introduction to Polynomial and Rational Functions

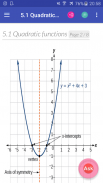
5.1. Quadratic Functions

5.2. Power Functions and Polynomial Functions

5.3. Graphs of Polynomial Functions

5.4. Dividing Polynomials

5.5. Zeros of Polynomial Functions

5.6. Rational Functions

5.7. Inverses and Radical Functions

5.8. Modeling Using Variation

6. Exponential and Logarithmic Functions

Introduction to Exponential and Logarithmic Functions

6.1. Exponential Functions

6.2. Graphs of Exponential Functions

6.3. Logarithmic Functions

6.4. Graphs of Logarithmic Functions

6.5. Logarithmic Properties

6.6. Exponential and Logarithmic Equations

6.7. Exponential and Logarithmic Models

6.8. Fitting Exponential Models to Data

7. Systems of Equations and Inequalities

Introduction to Systems of Equations and Inequalities

7.1. Systems of Linear Equations: Two Variables

7.2. Systems of Linear Equations: Three Variables

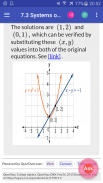
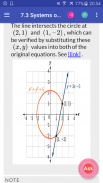
7.3. Systems of Nonlinear Equations and Inequalities: Two Variables

7.4. Partial Fractions

7.5. Matrices and Matrix Operations

7.6. Solving Systems with Gaussian Elimination

7.7. Solving Systems with Inverses

7.8. Solving Systems with Cramer's Rule

8. Analytic Geometry

Introduction to Analytic Geometry

8.1. The Ellipse

8.2. The Hyperbola

8.3. The Parabola

8.4. Rotation of Axes

8.5. Conic Sections in Polar Coordinates

9. Sequences, Probability, and Counting Theory

Introduction to Sequences, Probability and Counting Theory

9.1. Sequences and Their Notations

9.2. Arithmetic Sequences

9.3. Geometric Sequences

9.4. Series and Their Notations

9.5. Counting Principles

9.6. Binomial Theorem

9.7. Probability

College Algebra Lehrbuch von OpenStax und MCQ, Essay Fragen & Key Terms

College Algebra bietet eine umfassende Erforschung der algebraischen Prinzipien und erfüllt die Anforderungen Umfang und Abfolge für einen typischen Einführungs Algebra Kurs. Der modulare Ansatz und den Reichtum der Inhalte sicherzustellen, dass das Buch auf die Bedürfnisse einer Vielzahl von Kursen erfüllt. College Algebra bietet eine Fülle von Beispielen mit detaillierten, konzeptionelle Erklärungen, ein starkes Fundament in der Baustoff-, bevor die Schüler fragen, das anzuwenden, was sie gelernt haben.

* Preislehrbuch von OpenStax

* Multiple-Choice-Fragen (MCQ)

* Essay Fragen Flash Cards

* Key-Bedingungen Flash Cards

Angetrieben durch QuizOver.com der führenden Online-Quiz Schöpfer

https://www.quizover.com

1. Voraussetzungen

Einführung in die Voraussetzungen

1.1. Reelle Zahlen: Algebra-Grundlagen

1.2. Exponents und wissenschaftliche Schreibweise

1.3. Radikale und Rational Exponents

1.4. Polynomials

1.5. Factoring Polynomials

1.6. Rational Expressions

2. Gleichungen und Ungleichungen

Einführung in den Gleichungen und Ungleichungen

2.1. Die rechteckigen Koordinatensysteme und Graphen

2.2. Lineare Gleichungen in einer Variablen

2.3. Modelle und Anwendungen

2.4. Komplexe Zahlen

2.5. Quadratische Gleichungen

2.6. Andere Arten von Gleichungen

2.7. Lineare Ungleichungen und Absolutwert Ungleichungen

3. Funktionen

Einführung in die Funktionen

3.1. Funktionen und Funktions Notation

3.2. Domain und Range

3.3. Veränderungsraten und Verhalten von Graphen

3.4. Zusammensetzung der Funktionen

3.5. Die Transformation von Funktionen

3.6. Absolute Wertfunktionen

3.7. inverse Funktionen

4. Lineare Funktionen

Einführung in die Lineare Funktionen

4.1. lineare Funktionen

4.2. Modellierung mit Lineare Funktionen

4.3. Fitting lineare Modelle auf Daten

5. Polynomial und Rationale Funktionen

Einführung in die Polynomial und Rationale Funktionen

5.1. quadratische Funktionen

5.2. Power Functions und Polynomfunktionen

5.3. Graphen von Polynomfunktionen

5.4. Dividieren Polynomials

5.5. Zeros von Polynomfunktionen

5.6. rationale Funktionen

5.7. Umkehrungen und Radical Funktionen

5.8. Modellierung Variation Verwenden

6. Exponential und logarithmische Funktionen

Einführung in die exponentielle und logarithmische Funktionen

6.1. Exponentialfunktionen

6.2. Graphen von Exponentialfunktionen

6.3. logarithmische Funktionen

6.4. Graphen der logarithmischen Funktionen

6.5. logarithmisch Eigenschaften

6.6. Exponentielle und logarithmische Gleichungen

6.7. Exponentielle und logarithmische Modelle

6.8. Fitting Exponential-Modelle auf Daten

7. Die Systeme der Gleichungen und Ungleichungen

Einführung in die Systeme von Gleichungen und Ungleichungen

7.1. Lineare Gleichungssysteme: zwei Variablen

7.2. Lineare Gleichungssysteme: Drei Variablen

7.3. Die Systeme der nichtlinearen Gleichungen und Ungleichungen: Zwei Variablen

7.4. Partialbrüche

7.5. Matrices und Matrix-Operationen

7.6. Lösen von Systemen mit Gauß-Elimination

7.7. Lösen von Systemen mit Inverses

7.8. Systeme mit Cramer-Regel zu lösen

8. Analytische Geometrie

Einführung in die analytische Geometrie

8.1. die Ellipse

8.2. die Hyperbel

8.3. die Parabola

8.4. Die Drehung der Achsen

8.5. Kegelschnitt in Polarkoordinaten

9. Sequenzen, Wahrscheinlichkeit und Zählen Theory

Einführung in die Sequenzen, Probability and Counting Theory

9.1. Sequenzen und ihre Notationen

9.2. arithmetische Folgen

9.3. geometrische Sequenzen

9.4. Serie und ihre Notationen

9.5. Zählen Principles

9.6. Binomialsatz

9.7. Wahrscheinlichkeit